Heaps and Priority Queues

Prioritiy Queues

• A priority queue is another type of an abstract data type.
  • It serves as a collection of items. We may add items to this bag and remove items, but we may only interact with the smallest item of the bag.

/** (Min) Priority Queue: Allowing tracking and removal of 
  * the smallest item in a priority queue. */
  public interface MinPQ<Item> {
    /** Adds the item to the priority queue. */
    public void add(Item x);
    /** Returns the smallest item in the priority queue. */
    public Item getSmallest();
    /** Removes the smallest item from the priority queue. */
    public Item removeSmallest();
    /** Returns the size of the priority queue. */
    public int size();
}

• Imagine trying to actively keep an array containing the maximum or minimum values gathered over time. If we took a regular list structure, we would have to store the total $N$ items and then sort and find the $M$ largest or smallest elements
  • This would take $log(N\log N)$ time complexity and $N$ space complexity.
  • If we used a priority queue intead, we would only be working with $M$ complexity.
• Ex:

public List<String> unharmoniousTexts(Sniffer sniffer, int M) {
    ArrayList<String>allMessages = new ArrayList<String>();
    for (Timer timer = new Timer(); timer.hours() < 24; ) {
        allMessages.add(sniffer.getNextMessage());
    }

    Comparator<String> cmptr = new HarmoniousnessComparator();
    Collections.sort(allMessages, cmptr, Collections.reverseOrder());

    return allMessages.sublist(0, M);

• The above code is inefficient, we may use a priority queue however:

public MinPQ<String> unharmoniousTexts(Sniffer sniffer, int M) {
    MinPQ<String> unharmonious = new HeapMinPQ<>();

    for (Timer timer = new Timer(); timer.hours() < 24; ) {
        unharmonious.add(sniffer.getNextMessage());
        if (unharmonious.size() > M) {
            unharmonious.removeSmallest();
        }
    }

    return unharmonious;
}

• When we look at other data structure implementations we have, we note that a bushy BST gives us the best complexity amongst all our desired methods. It has $\Theta (\log N)$ complexity for add, getSmallest, and removeSmallest.

Heaps

• We want to implement a PQ using a binary tree. This tree must be complete and obey the min-heap property.
  • Min-heap: Every node is less than or equal to both of its children.
  • Complete: Missing items only at the bottom level (if any), all nodes are as far left as possible.

Heap Implementation

• add: We add to the end of the heap temporarily. We swim up the hierarchy to the proper place and we may swap nodes if the child happens to be lesser than the parent.
  • Swimming means that we keep moving along the edges of the tree until the new key that we added is greater than its parents. Very simple! Just trace up the parents hierarchy.
• getSmallest: Return the root of the heap. Min-heap guarantees that the root is the smallest value.
• removeSmallest: Swap the last item in the heap into the root. Sink the hierarchy to the proper place.
  • Sinking means that we swap nodes if the parent is greater than the child. We swap with the smallest child to preserve min-heap.

Implementations of Trees

• There are various implementation of trees that we may consider.

  Tree based Implementations

• Fixed-Width Nodes: Our tree is represented by Nodes and each node contains a specific key and references to its children.

public class Tree1A<K> {
    K k;
    Tree1A left;
    Tree1A middle;
    Tree1A right;
    ...
  }

• Variable-width Nodes: Our tree stores a value, and children are stored in variable length arrays.

public class Tree1B<Key> {
    Key k;
    Tree1B[] children;
    ...
}  

• Sibling Tree: Noddes maintain reference to their siblings like a linked list.

public class Tree1C<Key> {
    Key k;
    Tree1C favoredChild;
    Tree1C sibling;
    ...
  }

Array based implementations

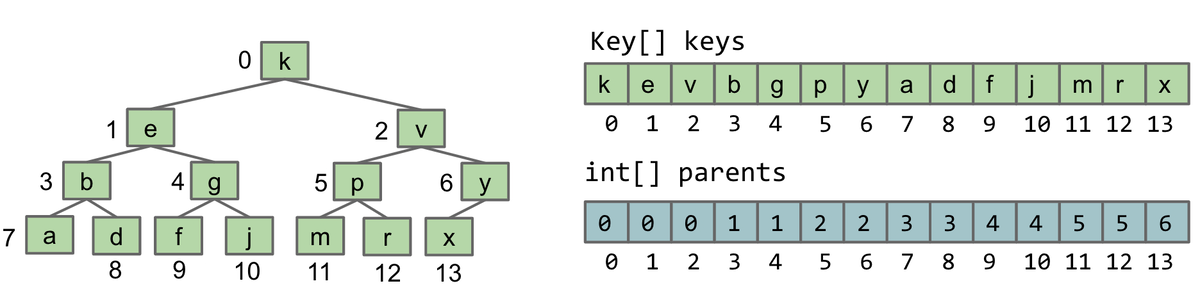
• Key and Parents Array: We keep track of all the keys by assigning each key an index in an array. We then keep track of the parents by storing another array of the same length, where each index contains the index of the parent key of that node.
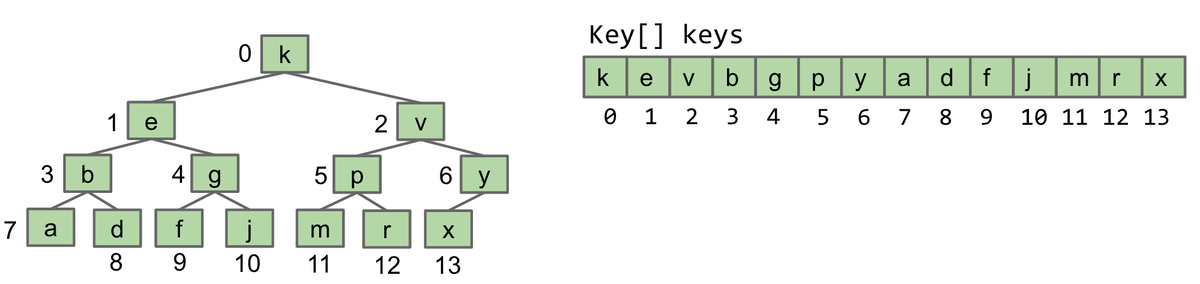
• However, we note that this implementation provides a lot of redundancy. The keys and the parents share a pattern in that two keys together share the same parent. We recall that a heap is a complete tree, meaning that it would never have a gap in itself. Thus, we could just compress our array based implementation into one array:
• Ultimately, this is how we may represent a heap as an array. Writing the swim and parent operations could proceed as such:

public void swim(int k) {
    if (keys[parent(k)] > keys[k]) {
        swap(k, parent(k));
    }
    swim(parent(k));
}

public int parent(int k) {
    return Math.max((k-1)/2, 0);
}

parent(4);

1

public class MinHeap<K extends Comparable<? super K>> implements MinPQ<K> {
    private K[] keys;
    private int size;

    public MinHeap() {
        this.keys = (K[]) new Comparable[32];
        this.size = 0;
    }
    /** Adds the item to the priority queue. */
    @Override
    public void add(K x) {
        if (size >= keys.length) {
            resize(2 * keys.length);
        }
        this.keys[this.size] = x;
        this.size += 1;
        swim(this.size - 1);
    }

    @Override
    public String toString() {
        return Arrays.toString(this.keys);
    }

    /** Returns the smallest item in the priority queue. */
    public K getSmallest() {
        return this.keys[0];
    };
    /** Removes the smallest item from the priority queue. */
    public K removeSmallest() {
        K returnValue = this.getSmallest();
        this.keys[0] = this.keys[this.size - 1];
        this.size -= 1;
        sink(0);
        return returnValue;
    }

    /** Returns the size of the priority queue. */
    public int size() {
        return this.size;
    };

    private void swim(int k) {
        if (k <= 0 || this.keys[this.parent(k)].compareTo(this.keys[k]) <= 0) {
            return;
        }
        if (this.keys[this.parent(k)].compareTo(this.keys[k]) > 0) {
            this.swap(k, this.parent(k));
        }
        this.swim(parent(k));
    }

    private void sink(int k) {
        while (2 * k + 1 < this.size()) {
            int smaller = getLeftChild(k);
            int rightChild = getRightChild(k);

            if (rightChild < this.size() && this.keys[rightChild].compareTo(this.keys[smaller]) < 0) {
                smaller = rightChild;
            }

            if (this.keys[smaller].compareTo(this.keys[k]) >= 0) {
                break;
            }
            swap(smaller, k);
            k = smaller;
        }
    }
    
    private int parent(int k) {
        return Math.max((k-1)/2, 0);
    }
    
    private void swap(int i, int j) {
        K temp = this.keys[i];
        this.keys[i] = this.keys[j];
        this.keys[j] = temp;
    }

    private int getLeftChild(int parent) {
        return parent * 2 + 1;
    }

    private int getRightChild(int parent) {
        return (parent + 1 ) * 2;
    }

    private void resize(int capacity) {
        K[] temp = (K[]) new Comparable[capacity];
        System.arraycopy(this.keys, 0, temp, 0, this.size);
        keys = temp;
    }
}

MinPQ<String> test = new MinHeap<>();
test.add("b");
test.add("c");
test.add("d");
test.add("e");
test.add("f");
test.add("g");
test.add("a");
test.toString();

[a, c, b, e, f, g, d, null, null, null, null, null, null, null, null, null, null, null, null, null, null, null, null, null, null, null, null, null, null, null, null, null]