CS61B: Lecture 18

Tree Rotation

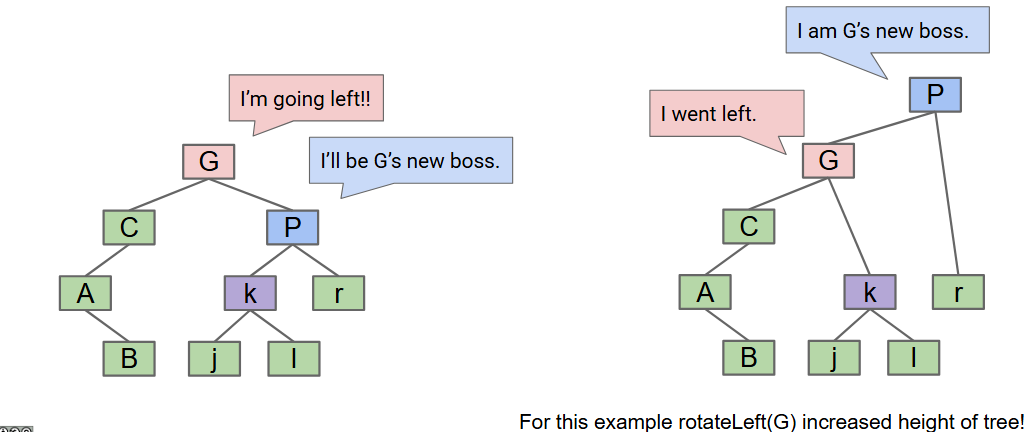
• We may reotate trees left or right to keep trees balanced. In fact, in any BST, it is possible to move to a different configuration using “rotation”.
• rotateLeft(G): let x be the right child of G. Make G the new left child of x.
  • X’s left child now becomes G’s right child.
• rotateRight(G): let x be the left child of G. Make G the new right child of x.
  • X’s right child now becomes G’s left child.
• These rotations can help us balance a tree.
  • The rotation preseves the search tree property.
  • We want to eventually reach a tree with the minimum average depth.
• The 2-3 tree can be used to model the rotations to self balance a binary search tree.
• There are many types of search trees:
  • Binary search Trees: Balanced by rotation but no existing algorithm for doing so yet.
  • 2-3 Trees: Balanced by construction: No rotation required.
  • We want to build a BST that is structurally identical to a 2-3 Tree

Writing a BST that is identical to a 2-3 Tree

• Such a BST is called a Red-Black Tree.
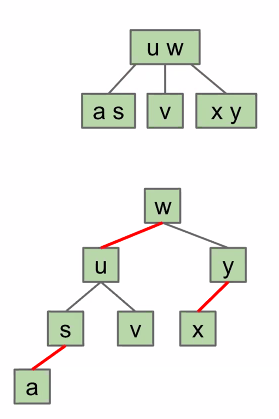
  • We color some of the link red. In a 2-3 Tree, we seperate a two node into a larger node whose left child is the smaller node along with all the children that are smaller than the larger node.
  • The nodes within a 3 node are connected with a left-leaning left edge from the greater node as the parent, and the lesser node as the left child.
• A BST with left glue links that represents that represents a 2-3 tree is called a “left Leaning Red Black Binary Search Tree
• Searching in an LLRB for a key is exactly the same as a BST.

LLRB Construction

• We don’t want to build a 2-3 tree and convert it.
• We want to implement an LLRB insert
  • Insert as usual into a BST, but then use zero or more totations to maintain a 1-1 mapping with the 2-3 Tree
  • Pretend like we are a 2-3 tree when we are doing rotations.
• Should we use a red or black link when inserting?
  • In 2-3 trees, new values are always added to a leaf node.
  • Insertion on the left: We add a red link to connect the new node as the left child of a leaf node.
  • Insertion on the right: We add the right child, and we realize that we have a 3 node in a 2-3 tree. Thus, we want to rotate the parent to the left so that we form a left-leaning, red edge.
  • Double Insertion on the left: This means that we have a
  • Temporary 4 node violation