CS61A: Trees

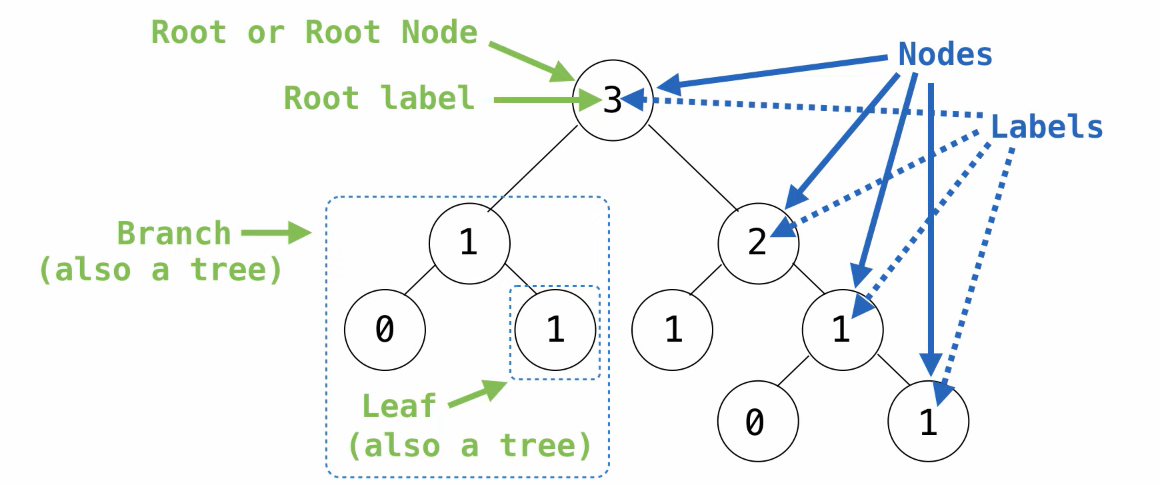
Trees

• A data abstraction used for representing hierarchical relationships.
  • Two different metaphors of a tree:
    • Recursive description (wooden trees):
      • A tree possesses a root label and a list of branches.
      • Each branch is a a tree, and also has a root label.
      • A tree with zero branches is a leaf
        • A leaf is also a tree
    • Relative description: (family trees):
      • Each location in a tree is called a node.
      • Each node has a label that can be any value.
      • One node can be the parent/child of another.
        • Ancestors, descendants, siblings, etc.
• People often refer to labels by their locations: “each parent is the sum of its children”
  

Implementing the Tree Abstraction

• A tree has a root label and a list of branches (this is for the constructor)
  • Each branch is a tree

def tree(label, branches=[]): # The default value of branches has nothing. So by default, we create a leaf of a tree
    for branch in branches:
        assert is_tree(branch) # Make sure that all branches are trees
    return [label] + list(branches) # Ensure that any sequence of trees is converted into a list

def label(tree):
    return tree[0]

def branches(tree):
    return tree[1:]

def is_tree(tree):
    if type(tree) != list or len(tree) < 1:
        return False
    for branch in branches(tree):
        if not is_tree(branch):
            return False
    return True

def is_leaf(tree):
    return not branches(tree)

from tree import tree
tree(3, [tree(1), tree(2, [tree(1), tree(1)])])

[3, [1], [2, [1], [1]]]

Tree Processing

• Any function that takes in a tree as an input or returns a tree is likely tree recursive as well.
• Tree are typically generated programmatically, for instance, a fibonacci tree:

def fib_tree(n):
    if n <= 1:
        return tree(n)
    left, right = fib_tree(n-2), fib_tree(n-1)
    return tree(label(left) + label(right), [left, right])

fib_tree(4)

[3, [1, [0], [1]], [2, [1], [1, [0], [1]]]]

Tree Processing Uses Recursion

• In most tree processing functions, processing a leaf is the base case.
  • Recursive case makes a recursive call on each branch, then aggregates the results.

def count_leaves(t):
    """Count the leaves of a tree."""
    if is_leaf(t):
        return 1
    return sum([count_leaves(branch) for branch in branches(t)])

count_leaves(fib_tree(4))

5

Discussion Question 1

• Implement leaves, which returns a list of the leaf labels of a tree

def leaves(tree):
    if is_leaf(tree):
        return [label(tree)]
    return sum([leaves(branch) for branch in branches(tree)], [])

leaves(fib_tree(5))

[1, 0, 1, 0, 1, 1, 0, 1]

Creating Trees

• A function that creates a tree from another tree is typically also recursive

def increment_leaves(t):
    """Return a tree like t but with leaf labels incremented."""
    def helper(t):
        if is_leaf(t):
            return tree(label(t) + 1)
        return tree(label(t), [helper(branch) for branch in branches(t)])
    return helper(t)

print(fib_tree(4))
print(increment_leaves(fib_tree(4)))

[3, [1, [0], [1]], [2, [1], [1, [0], [1]]]]
[3, [1, [1], [2]], [2, [2], [1, [1], [2]]]]

def increment(t):
    """Return a tree like t but with leaf labels incremented."""
    return tree(label(t) + 1, [increment(branch) for branch in branches(t)])

print(fib_tree(4))
print(increment(fib_tree(4)))

[3, [1, [0], [1]], [2, [1], [1, [0], [1]]]]
[4, [2, [1], [2]], [3, [2], [2, [1], [2]]]]

Example: Printing Trees

def print_tree(t, level=0):
    print(level * "   " + "|--" + str(label(t)))
    for b in branches(t):
        print_tree(b, level+1)

print_tree(fib_tree(6))

|--8
   |--3
      |--1
         |--0
         |--1
      |--2
         |--1
         |--1
            |--0
            |--1
   |--5
      |--2
         |--1
         |--1
            |--0
            |--1
      |--3
         |--1
            |--0
            |--1
         |--2
            |--1
            |--1
               |--0
               |--1

Example: Summing Paths

• Some recursive functions build up their result by manipulating the return values of a recursive call.
• Other recursive functions build up their results by passing information into the recursive call as an argument.
• Ex: Factorial

def fact(n):
    if n == 0:
        return 1
    else:
        return n * fact(n-1) # manipulating the return value of a recursive call.
    
def fact_times(n, k):
    """Returns k * n * (n-1) * ... * 1"""
    if n == 0:
        return k
    else:
        return fact_times(n-1, k * n) # Result of the recursive call is the result of the current call.
    

• In fact_times, the result is being built up with each recursive call, until we hit the base case, which just returns the solution.
  • In fact all the multiplying occurs after we’ve hit the base case.
• We can apply similar recursive logic to trees

from tree import *

numbers = tree(3, [tree(4), tree(5, [tree(6)])])
haste = tree("h", [tree("a", [tree("s"), tree("t")]), tree("e")])

def print_sums(t, sum_so_far):
    if is_leaf(t):
        print(sum_so_far + label(t))
    for branch in branches(t):
        print_sums(branch, sum_so_far+label(t))

print_sums(haste, "")

has
hat
he

Example: Counting Paths

• Create a function that count the number of paths within a tree that have a total label sum.

def count_paths(t, total):
    """Return the number of paths from the root to any node in tree t for which the labels along the path sum to total."""
    if total-label(t) == 0:
        found = 1
    else:
        found = 0
    return found + sum([count_paths(branch, total-label(t)) for branch in branches(t)])

t = tree(3, [tree(-1), tree(1, [tree(2, [tree(1)]), tree(3)]), tree(1, [tree(-1)])])
count_paths(t, 3)

2