Order of Recursive Calls
- When ever a function call is made, it must return before we can do something.
- What ever is after the recursive call is executed after the recursion ends
- The Casecade Function:
1
2
3
4
5
6
7
8
9
10
def cascade(n):
if n < 10:
print(n)
else:
print(n)
cascade(n//10)
print(n)
cascade(1234)
1
2
3
4
5
6
7
1234
123
12
1
12
123
1234
- In recursive function calls, the first return value will be the base case, then followed up by all the pre-exisiting recursive calls, back to the first call.
- We must trace our recursive calls back up to the original call.
- Until the return value appears for a recursive call, that call is incomplete.
- Each cascade frame is a different call to cascade in and of itself.
- statements can appear before and after the recrusive call.
- A shorter version of cascade:
1
2
3
4
5
6
7
def cascade(n):
print(n)
if n > 10:
cascade(n//10)
print(n)
cascade(12345)
1
2
3
4
5
6
7
8
9
12345
1234
123
12
1
12
123
1234
12345
- Typically, the shorter implementation is better to understand.
- Always put the base cases first in recursive functions first
Example: Inverse Cascade
- My Intution: We first make recursive calls until the base case, where we then print out each subsequent value
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def inverse_cascade(n):
grow(n)
print(n)
shrink(n)
def f_then_g(f, g, n):
if n:
f(n)
g(n)
grow = lambda n: f_then_g(grow, print, n//10)
shrink = lambda n: f_then_g(print, shrink, n//10)
inverse_cascade(1234)
1
2
3
4
5
6
7
1
12
123
1234
123
12
1
- Implementations of grow and shrink
- For grow: We recursively call itself until n becomes one digit, from where we print and unravel the sequence
- For shrink: We recursively call itself at each step with a print statement, then continue onto the next recursive call.
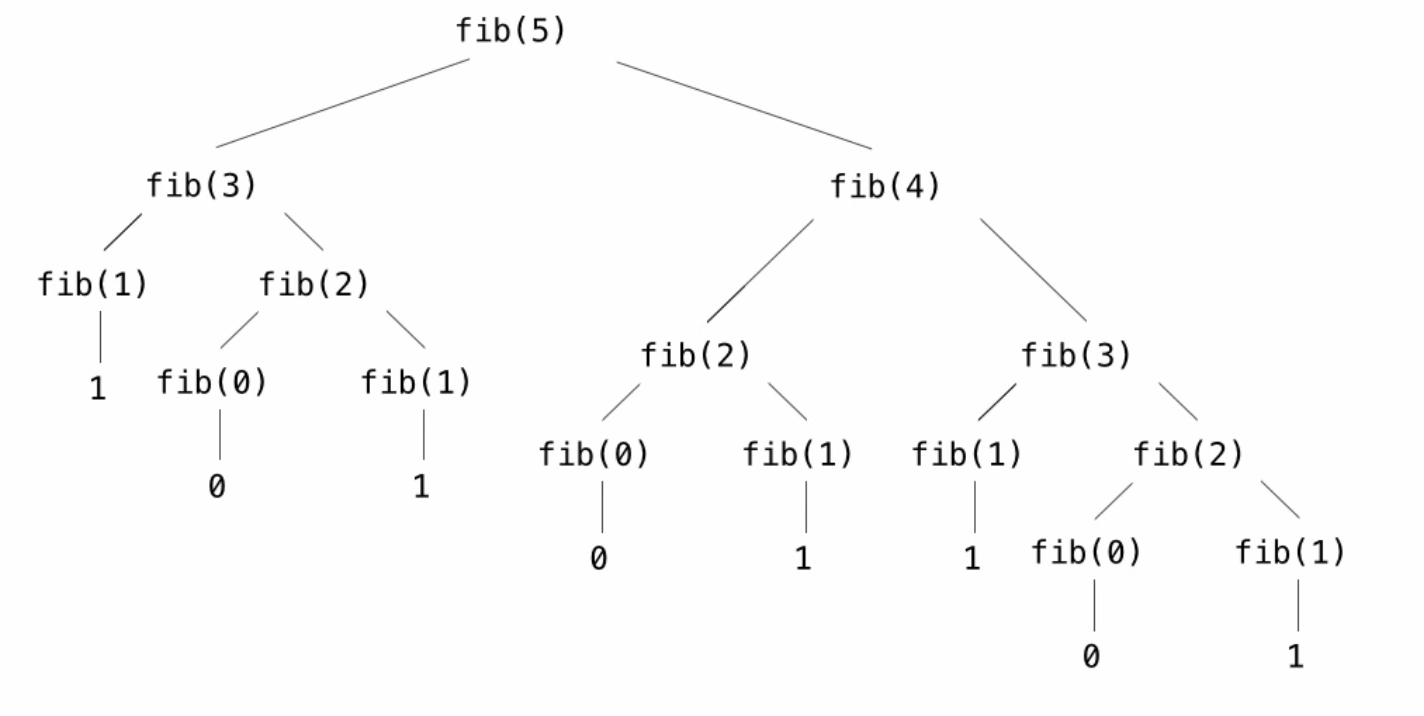
Tree Recursion
- Recursive functions can make more than one recursive call to itself. (Think of mergeSort)
- When this happens, function produces tree-shaped processes.
- Classic example was the fibonacci numbers.
- n: 0, 1, 2, 3, 4, 5, 6, 7, 8, …, 35
- fib(n): 0, 1, 1, 2, 3, 5, 8, 13, 21, …, 9,227,465
- The Sequence can be calculated with Tree Recursion
1
2
3
4
5
6
7
def fib(n):
if n == 0:
return 0
if n == 1:
return 1
else:
return fib(n-2) + fib(n-1) # Because fib itself is called twice recursively, this creates a tree process
- The runtime of this function can be described by this following tree process:
1
fib()
Repitition in Tree-Recursive Computation
- There is a lot of repitition in tree-recursive computation. In Fib, we repeated calculations everytime we went up to a higher number.
- Fib is called on the same argument multiple times.
- This process can be sped up dramatically in a few weeks by remembering the results of each function call, and reusing that.
Example Counting Partitions
- Hard process to write without tree recursions.
The number of partitions of a positive inter n, using parts up to size m, is the number of ways in which n can be expressed as the sum of positive integer parts up to m in increasing order.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
from ucb import trace
# @trace
def counting_partitions(n, m):
if m == 0:
return 0
if m > n:
return 0 + counting_partitions(n, m-1)
if m == n:
return 1 + counting_partitions(n, m-1)
return counting_partitions(n-m, m) + counting_partitions(n, m-1)
# @trace
def counting_partitions_2(n, m):
if n < 0: # We reach the end of a unsuccessful equation, n-m < 0 in function call
return 0
if n == 0: # counts every successful equation
return 1
return counting_partitions(n-m, m) + counting_partitions(n, m-1) # Add the possible solutions to n-m with m, and then m-1
def counting_partitions_iter(n, m):
dp = [[0] * (m + 1) for k in range(n + 1)]
dp[0][0] = 1
for i in range(1, n + 1):
for j in range(1, m + 1):
if j > i:
dp[i][j] = dp[i][j-1]
elif i == j:
dp[i][j] = dp[i][j-1] + 1
else:
dp[i][j] = dp[i-j][j] + dp[i][j-1]
return dp[n][m]
# [1,0,0,0,0,0,0]
print(counting_partitions_2(6,4))
print()
counting_partitions_iter(6,4)
1
2
3
4
5
6
7
8
9
9
- Start with recursive decomposition: find simpler instances of the problem.