CS61A: Recursion

Self-Reference

• In environments, functions may refer to their own name within the body (how environments are designed to be)

def print_all(x):
    print(x)
    return print_all # Doesn't call itself

print_all(1)(2)(3)

1
2
3





<function __main__.print_all(x)>

• Whenever a function calls itself within its body, it creates a new frame of that function.
  • If print_all did call itself with an argument instead of returning itself, then we would run forever, (or hit maximum recursion depth)

def print_sums(x):
    print(x)
    def next_sum(y):
        return print_sums(x+y)
    return next_sum

print_sums(1)(2)(5)(7)

1
3
8
15





<function __main__.print_sums.<locals>.next_sum(y)>

• Interestingly, in the above example, recursive calls may also be defined within nested functions. next_sum is the function doing the recursion.
  • What I think: This technique is useful for doing mult-line operations on a function’s previous argument before the recursive call is executed.
  • Also, using a nested statement allows us to memorize the previous arguments in recursion. The function that is returned has a reference to the previous frame in which it is defined.
• The first call in print_sums(1)(2)(3), that is, print_sums(1) is a call to print_sums itself. The other two calls, that is, (2)(3) are called on the function that print_sums returns, which isn’t necessarily itself, but rather a nested function next_sum that does preprocessing before calling print_sums itself.

Recursive Functions

• Definition: A function is recursive if the body of the function calls itself, whether it be directly or indirectly (through an nested function)
• Implication: Executing the body of a recursive may require applying that function again. Depending on the input arguments.

Digit Sums

• Sums of the digit 2013 is 2+0+1+3 = 6.
• For any given number a, if a is divisible by 9, then digit_sum(a) is also divisible by 9.
  • Usecase: Typo detection. The 16th digit, the checksum number, is not part of the account number, but instead computed from the other digits. If the checksum digit does not match the computation (Luhn algorithm) of the other digits, then the card number is invalid.

Sum Digits Without a While Statement

def split(n):
    """Split positive n into all but its last digit and its last digit."""
    return n // 10, n % 10

def sum_digits(n):
    """Return the sum of the digits of positive integer n."""
    if n < 10:
        return n
    else:
        all_but_last, last = split(n)
        return sum_digits(all_but_last) + last
    
sum_digits(2024)

8

Anatomy of a Resursive Function

• def statement header still binds the function to its intrinsic name
• Conditional statements exist within the function to check for base cases, or where the function should stop recursing to prevent infinite recursion.
  • Base cases are trivial/simple cases to solve.
• Base cases are evluated without recursive calls and can be computed directly.
• If the input is complex (not a base case), then it is a recursive case that is evaluated with recursive calls.

Recursion in Environment Diagrams

• Implement the factorial function:

def fact(n):
    if n == 0:
        return 1
    else:
        return n * fact(n-1)

fact(3)

6

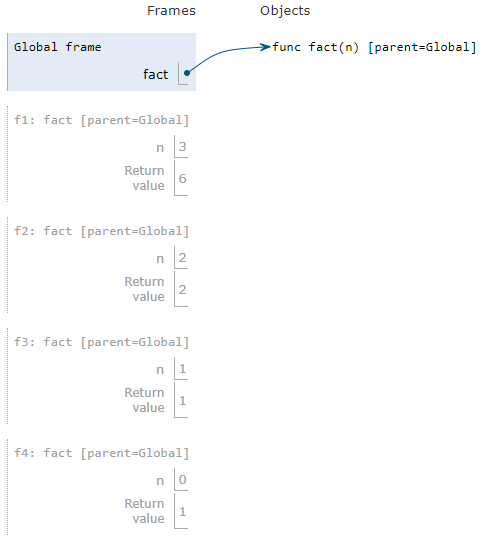
• Environmental Diagram:
  
• With every recursive call, we open up a new frame.
• When the return statement is called, we take the value back with us to the line in the frame of our program where the function was executed.
• The return value is then used in the computation of the return value of the function above the returned function in the recursion tree.
• Properties of recursion in environmental diagramsL
  • The same function is called multiple times
  • Different frames keep track of the different arguments with each call.
  • What n evaluates to depends on the current environment.
  • Every call of fact solves a simpler computational problem than the last call: which in this case is a smaller value of n.
    • THIS IS AT THE CORE OF DIVIDE AND CONQUER ALGORITHMS!!!

Iteration vs Recursion

• Iteration is a special case of recursion

def fact_iter(n):
    total, k = 1, 1
    while k <= n:
        total, k = total*k, k+1
    return total

def fact(n):
    if n == 0:
        return 1
    else:
        return n * fact(n-1)
    
fact_iter(4) == fact(4)

True

• The code with recursion makes much more intuitive and logical sense. It has a shorter implementation that clearly marks out what each step of recursion does.
• Mathematically:
  • Iteration: \(n! = \prod_{k=1}^{n}k\)
  • Recursion: \(n! = \left\{ \begin{array}{cl} 1 & : \ \text{if } n = 0 \\ n \cdot (n-1)! & : \ \text{otherwise} \end{array} \right.\)
  • Both definition produces the same result, jsut the iteration includs extra machinery to keep track of the total.
    • The complexity is much lower in recursion, as the number of names are much less as our current values are kept tracked by the frames and environmental diagram

Verifying Recursive Functions

• The Recursive Leap of Faith
  • We must trust if our recursion works properly, and there are steps to help with that: 1) Verify the base case. 2) Treat the function as a functional abstraction. Do not care about implementation, just what it is supposed to do. 3) Assume that recursive_function(next_case) is correct (function is correctly defined for simpler case in recursive calls) 4) Confirm that recursive_function(n) is correct based on our assumption that recursive_function(next_case) is correct
  • The method above is very similar to inductive proofs!

Mutual Recursion

• Two different functions call each other

The Luhn Algorithm

• Used to verify the checksum of credit cart numbers
  1. From the right most digit, which is the check digit, moving left, double the value of every second digit; if product of this doubling operation is greater than 9 (e.g., 7 * 2 = 14), then sum the digits of the products (e.g., 10: 1 + 0 = 1, 14: 1 + 4 = 5).
  2. Take the sum of all the digits
     • Ex: [1, 3, 8, 7, 4, 3] -> [2,3,16,7,8,3] -> [2,3,7,7,8,3] -> sum([2,3,7,7,8,3]) = 30
  3. The Luhn sum of a valid credit card number is a multiple of 10.

def luhn_sum(n):
    if n < 10:
        return n
    else:
        all_but_last, last = split(n)
        return luhn_sum_double(all_but_last) + last

def luhn_sum_double(n):
    all_but_last, last = split(n)
    luhn_digit = sum_digits(2 * last)
    if n < 10:
        return luhn_digit
    else:
        return luhn_sum(all_but_last) + luhn_digit 
    
luhn_sum(4833160288226712)

70

• The implementation of luhn_sum and luhn_sum_double above is an example of mutual recursion where two functions are calling each other.
  • In this case, base cases already exist in both functions.

Converting Recursion to Iteration… and Back Again

• Iteration is a special case of recursion
  • Figure out what state must be maintained by the iterative function at each stage of iteration.
• The reverse could also work for converting iteration to recursion
  • The state of each iteration can be passed as arguments
  • The state in sum_digits_iter is n, which represents the remaining digits in our calculation.

def sum_digits(n):
    """Return the sum of the digits of positive integer n."""
    if n < 10:
        return n
    else:
        all_but_last, last = split(n)
        return sum_digits(all_but_last) + last # all_but_last is the digits remaining, while last is a partial sum
    
def sum_digits_iter(n):
    digit_sum = 0
    while n > 0: # n itself is the digits remaining
        n, last = split(n)
        digit_sum += last # last is the partial sum we are adding
    return digit_sum

def sum_digits_rec(n, digit_sum): # The state contains both the n and the digit_sum
    if n == 0:
        return digit_sum
    n, last = split(n) 
    return sum_digits_rec(n, digit_sum+last)

sum_digits(1337) == sum_digits_iter(1337) == sum_digits_rec(1337, 0)

True