Home CS61A: Composition
Post
Cancel

CS61A: Composition

Posted Oct 21, 2024
By Alexander Lu
8 min read

Linked Lists

  • A type of recursive data structure that stores a sequence of values.
  • A linked list is either
    • empty
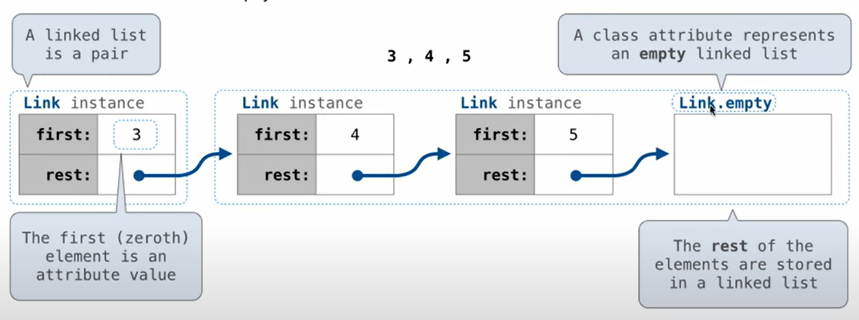
    • a first value and the rest of the linked list
  • Thus, any non-empty linked list contains the value at the current node, and a smaller linked-list that represents the rest of the list.
    Linked List Structure
  • The concept of composition is used to create the structure of a linked list.
    • Composition: The act of assigning an object to an attribute of another object.
  • For 61A, we construct linked lists in the following manner:
    • Link(3, Link(4, Link(5, Link.empty)))
    • To evaluate this expression, we must first evaluate the linked list for the last node 5, then node 4, and then the node 3.
  • Implementation:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Link:
    # Empty tuple as it has a length of 0
    empty = ()
    def __init__(self, first, rest=empty):
        # We must ensure that rest is either a Link instance, or Link.empty
        assert rest is Link.empty or isinstance(rest, Link)
        self.first = first
        self.rest = rest

    def __repr__(self):
        if self.rest:
            rest_repr = ', ' + repr(self.rest)
        else:
            rest_repr = ''
        return 'Link(' + repr(self.first) + rest_repr + ')'
    
    def __str__(self):
        string = '('
        while self.rest is not Link.empty:
            string = string + str(self.first) + "->"
            self = self.rest
        return string + str(self.first) + ")"
  • In the implementation above, we used the isinstance function to test if an object is an instance of a class or of the subclass of a class.
    • In other words, we can also have rest be an instance of a subclass of Link.
    • This enables us more flexibility in our implementation.
  • Ex:
1
2
3
4
5
6
7
8

s = Link(3, Link(4, Link(5)))
print("s.first:", s.first)
print("s.rest:", s.rest)
print("s.rest.first:", s.rest.first)
print("s.rest.rest.first:", s.rest.rest.first)
s.rest.first = 7
print("Updated the second value of s to 7")
print("s:", s)

1
2
3
4
5
6

s.first: 3
s.rest: (4->5)
s.rest.first: 4
s.rest.rest.first: 5
Updated the second value of s to 7
s: (3->7->5)
  • It is very efficient to create new linked lists from old linked lists, as all we need to do is change or add new references.
1
2
3
4
5

# We want to create a new Linked list that has the values of 3,7,6,5
t = s
new_node = Link(6, t.rest.rest)
t.rest.rest = new_node
print(t)

1

(3->7->6->5)

Linked List Processing

  • Recursion is commonly used in linked list processing

Example: Range, Map and Filter for Linked Lists

  • We want to create map_link, filter_link, and range_link such that:
1
2

square, odd = lambda x: x**2, lambda x: x%2==1
map_link(square, filter_link(odd, range_link(1,6))) -> Link(1, Link(9, Link(25)))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

square, odd = lambda x: x * x, lambda x: x%2==1
def range_link(start, end):
    """Return a Link containing consecutive intergers from start to end.
    
    >>> range_link(3, 6)
    Link(3, Link(4, Link(5)))
    """
    if start >= end:
        return Link.empty
    return Link(start, range_link(start+1, end))

def filter_link(func, ll):
    """Return a Link that contains only the elements x of Link ll for which f(x) is a true value.
    
    >>> filter_link(odd, range_link(3, 6))
    Link(3, Link(5))
    """
    if ll == Link.empty:
        return ll
    elif func(ll.first):
        return Link(ll.first, filter_link(func, ll.rest))
    return Link(ll.rest.first, filter_link(func, ll.rest.rest))

def map_link(func, ll):
    """Return a Link that contains f(x) for each x in Link ll.
    
    >>> map_link(square, range_link(3, 6))
    Link(9, Link(16, Link(25)))
    """
    if ll == Link.empty:
        return ll
    return Link(func(ll.first), map_link(func, ll.rest))

map_link(square, filter_link(odd, range_link(1, 6)))


1

Link(1, Link(9, Link(25)))
  • For the most part, my implementation is consistent with DeNero’s. However, we did differ on the filter_link implementation
1
2
3
4
5
6
7
8
9

def denero_filter_link(func, ll):
    if ll is Link.empty:
        return ll
    filtered_rest = denero_filter_link(func, ll.rest)
    if func(ll.first):
        return Link(ll.first, filtered_rest)
    return filtered_rest

map_link(square, denero_filter_link(odd, range_link(1, 6)))

1

Link(1, Link(9, Link(25)))

Linked List Mutation

  • Because a linked list is an user-defined class, all of its attributes may be changed or mutated.
  • We may change the first and rest attributes of a Link
    • The rest of a linked list may contain the linked list as a sub-list
    • What we would have then is a cyclical linked-list
  • Ex:
1
2
3
4
5

s = Link(1, Link(2, Link(3)))
s.first = 5
t = s.rest
t.rest = s
s.rest.rest.rest.rest.rest.rest.rest.first # returns 2

1

2
  • Here is the flow of the program:
    • s is defined as 1->2->3
    • s is modified to 5->2->3
    • t is created as a reference to s.rest
    • t.rest is set to s itself, so s.rest.rest = s
    • thus, s = 5->2->5->2->5->2->5->2…

Linked List Mutation

  • Ex: Add an element into the appropriate position in an ordered linked-list with no repeats
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def add(ll, v):
    """Add v to an ordered list ll with no repeats, returning modified ll."""
    if ll is Link.empty:
        return Link(v)
    elif ll.first == v:
        return Link(ll.first, ll.rest)
    elif ll.first > v:
        return Link(v, ll)
    else:
        return Link(ll.first, add(ll.rest, v))

s = Link(1, Link(3, Link(4)))
s = add(s, 0)
s = add(s, 2)
s = add(s, 3)
s = add(s, 5)
s

1

Link(0, Link(1, Link(2, Link(3, Link(4, Link(5))))))
  • My implementation was a little bit different from DeNero’s implementation:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

def denero_add(ll, v):
    assert s is not Link.empty
    if ll.first > v:
        ll.first, ll.rest = v, Link(ll.first, ll.rest)
    elif ll.first < v and ll.rest is Link.empty:
        ll.rest = Link(v)
    elif ll.first < v:
        denero_add(ll.rest, v)
    return ll

s = Link(1, Link(3, Link(4)))
s = denero_add(s, 0)
s = denero_add(s, 2)
s = denero_add(s, 3)
s = denero_add(s, 5)
s

1

Link(0, Link(1, Link(2, Link(3, Link(4, Link(5))))))

Tree Class

  • The tree class is anothe recursive computational data structure.
  • We may either think about trees recursively (subtress) or relatively (parents and childs)
  • A path is a sequence of nodes where each element is either the parent or child of a previous nodes.
  • A Tree has a label and a list of branches where each branch is also a Tree
  • Thus, we may also define a tree using composition and OOP.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Tree:
    def __init__(self, label, branches = []):
        self.label = label
        for branch in branches:
            assert isinstance(branch, Tree)
        self.branches = list(branches)
    
    def __repr__(self):
        if self.branches:
            branch_str = ', ' + repr(self.branches)
        else:
            branch_str = ''
        return 'Tree({0}{1})'.format(repr(self.label), branch_str)
    
    def __str__(self):
        return '\n'.join(self.indented())
    
    def indented(self):
        lines = []
        for b in self.branches:
            for line in b.indented():
                lines.append('  ' + line)
        return [str(self.label)] + lines
    
    def is_leaf(self):
        return not self.branches

1

Tree(1)

1

Tree(1)

1
2

t = Tree(1, [Tree(3), Tree(4)])
t

1

Tree(1, [Tree(3), Tree(4)])

1

print(t)

1
2
3

1
  3
  4
  • Now, we try to create a function to generate a fib_tree
1
2
3
4
5
6
7
8
9

def fib_tree(n):
    """A fib tree"""
    if n < 2:
        return Tree(n)
    left = fib_tree(n-2)
    right = fib_tree(n-1)
    return Tree(left.label + right.label, [left, right])

print(fib_tree(6))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

8
  3
    1
      0
      1
    2
      1
      1
        0
        1
  5
    2
      1
      1
        0
        1
    3
      1
        0
        1
      2
        1
        1
          0
          1
  • We now try to write a functoin that computes a list of leaf labels in a Tree T
1
2
3
4
5
6
7

def leaves(t):
    """Return a list of leaf labels in Tree T."""
    if t.is_leaf():
        return [t.label]
    return sum([leaves(b) for b in t.branches], [])

leaves(fib_tree(6))

1

[0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1]

1
2
3
4
5
6
7
8
9
10

def denero_leaves(t):
    if t.is_leaf():
        return [t.label]
    else:
        all_leaves = []
        for b in t.branches:
            all_leaves.extend(leaves(b))
        return all_leaves
    
denero_leaves(fib_tree(6)) == leaves(fib_tree(6))

1

True
  • Finally, we write a function to calculate the height of a tree
1
2
3
4
5
6
7

def height(t):
    """Return the number of transitions in the longest path in T."""
    if t.is_leaf():
        return 0
    return 1+max([height(b) for b in t.branches])

height(fib_tree(6))

1

5

Tree Mutation

  • Tree pruning is when we remove certain subtrees from a tree.
    • Prune the branches before recursively pruning the branches of branches
  • Ex: Prune all sub-trees whose label is n
1
2
3
4
5
6
7
8
9

def prune(t, n):
    """Prne all sub-trees whose label is n."""
    t.branches = [b for b in t.branches if b.label != n]
    for b in t.branches:
        prune(b, n)

t = fib_tree(4)
prune(t, 1)
print(t)

1
2

3
  2
CS61A
CS61A Linked Lists OOP Composition
This post is licensed under CC BY 4.0 by the author.
Contents

CS61A: Representation

CS61A: Efficiency